„Gesunde Entwicklung ist ein kokreativer, mehrdimensionalerund evolutionärer Vorgang.“

„Ich bin ein evolutionär gewordener Teil größerer Lebensdimensionen. Ich lebe in stimmiger Verbundenheit und Resonanz mit diesen.“
3. Komplexe dynamische Systeme
Um Komplexität zu erfassen, braucht es einen ganzheitlichen systemischen Ansatz. In einer systemischen Sichtweise (Systemtheorie) spielt die Ganzheit eine zentrale Rolle.
Üblicherweise werden als Kriterien für komplexe Systeme genannt: Wechselwirkungen, Zirkularität, Unvorhersehbarkeit, Mehrdimensionalität, Selbstorganisation u. a.
Ein wichtiger Aspekt von Komplexität lässt sich an komplexen Zahlen verdeutlichen. Komplexe Zahlen haben außer reellen Zahlen 0, 1, 2, 3 usw. noch einen imaginären Anteil [1]. Eine imaginäre Einheit ist i = Wurzel aus –1; reell gibt es diese Zahl als Menge nicht. Sie existiert nur in der Imagination, ist also von gänzlich abstrakter Natur. Analog ist ein System als komplex zu bezeichnen, wenn es eine Kombination aus Realität und imaginierter (vorgestellter; nicht zählbarer, nicht physisch reeller) Information ist. In der Mathematik spricht man bei imaginären Zahlen auch von der „Erweiterung des Körpers (der reellen Zahlen)“. Analog dazu ist der Begriff komplexe Systeme zu verstehen als Erweiterung von beobachtbaren messbaren Systemen um funktionelle, abstrakte und imaginierte Zusammenhänge. Diese können nichtlineare und nichtlokale dynamische Entwicklungen beinhalten, die allerdings sehr wohl im wirksamen Zusammenhang mit realen Phänomenen stehen.
Unsere Logiken und Konstrukte in Zeichensystemen können grundsätzlich nur Annäherungen an die Komplexität wirklicher Systeme sein [2]. Deshalb können wir angesichts von komplexen lebenden Systemen in Demut denken und in der Lage sein, mit einer Rest-Ungewissheit umzugehen. Ungewissheit erfordert Vertrauen – das ist im Zusammenhang mit gesunder Entwicklung ein wichtiges alltägliches Thema, das in der Corona-Krise für sehr viele Menschen deutlich geworden ist – auch und ganz besonders für Wissenschaftlerinnen.
Kohärenz von komplexen Systemen
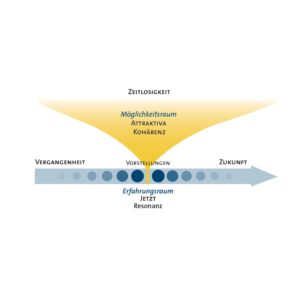
Die Kohärenz komplexer Systeme hat zwei unterschiedliche Aspekte: (1) Die realen, historisch entstandenen Bindungen, Beziehungen, die das System aktuell beobachtbar zusammenhalten. Diese entsprechen dem Beobachteten, dem Ausdruck, der Qualität und dem ganzen System. Wenn die Wahrnehmung dieser Realität in unser Bewusstsein kommt, ist sie schon Vergangenheit. Und (2) die gegenwärtigen Attraktiva, denen das System sich (immer wieder) anzunähern trachtet. Dies ist der imaginierte wie imaginäre Teil des Systems und betrifft seine Entwicklung in die Zukunft. Attraktiva sind Annäherungsziele, für Menschen beispielsweise Ideale, die eine dynamische Annäherung anregen. Die Kooperationen der Teilsysteme dienen dieser Attraktiva (s. a. Füllsack 2011). 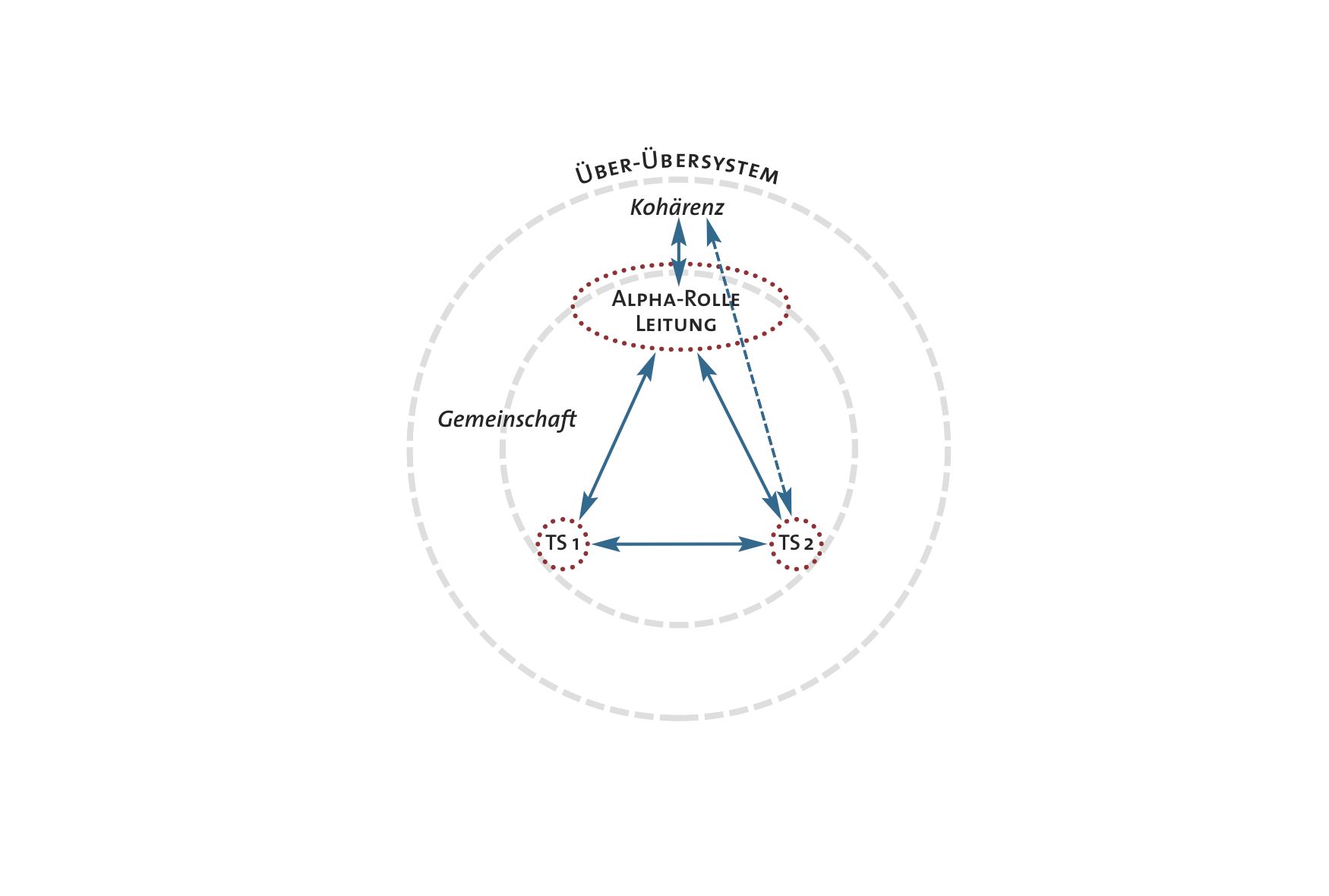
Abbildung 7: Macht und Einfluss der persönlichen Vertreter eines Systems. Die Kommunikation und Kooperation der Teilsysteme findet in der Kohärenz des Übersystems statt. Dadurch wird diese Kohärenz hergestellt und aufrechterhalten. Die Leitung vertritt in ihrer Funktion die Macht und Verantwortung des gemeinsamen Übersystems. Dabei steht sie auch in Resonanz zu größeren Übersystemen wie besonders der Kultur. Teilsysteme können auch in Resonanz zu ihren Über-Übersystemen wahrnehmen und agieren – mitwissen und handeln.
[1] Gottfried Wilhelm Leibniz nannte sie 1702 eine feine und wunderbare Zuflucht des menschlichen Geistes, beinahe ein Zwitterwesen zwischen Sein und Nichtsein. (Wikipedia: Komplexe Zahl)
[2] Der Gödelsche Unvollständigkeitssatz ist einer der wichtigsten Sätze der modernen Logik. Genauer werden zwei Unvollständigkeitssätze unterschieden. Der Erste Unvollständigkeitssatz besagt, dass es in hinreichend starken widerspruchsfreien Systemen immer unbeweisbare Aussagen gibt. Der Zweite Unvollständigkeitssatz besagt, dass hinreichend starke widerspruchsfreie Systeme ihre eigene Widerspruchsfreiheit nicht beweisen können.Durch diese Sätze ist der Mathematik eine prinzipielle Grenze gesetzt: Nicht jeder mathematische Satz kann aus den Axiomen eines mathematischen Teilgebietes (zum Beispiel Arithmetik, Geometrie und Algebra) formal abgeleitet oder widerlegt werden. In der Wissenschaftstheorie und in anderen Gebieten der Philosophie zählt der Satz zu den meist rezipierten der Mathematik. (Gödel 1931)
Die Marmor-Skulptur „Kommunikation“ (im Header-Foto der Startseite) ist von Dietlind Petzold: www.studio-amaranta.com.
